|
Nonlinear Dynamics at the Free University Berlin | |||||||||||||||||||||||||||||||||||||||
|
Organization
Welcome Activities
Publications Research Group Nonlinear Dynamics
Dr. A. López-Nieto |
Bifurcations without parameters(Bernold Fiedler, Stefan Liebscher, James C. Alexander) See also the Picture Gallery of the Dynamical Systems Web. AbstractThe following pictures illustrate some elements of the nonlinear dynamics near equilibrium manifolds. Denoting the equilibrium manifold by x=0, in local coordinates (x, y) in Rn x Rk, we consider systems
and assume
for all y. For simplicity we will only address the cases k=1 of lines of equilibria. Sufficient smoothness of f and g is assumed. The occurrence of equilibrium manifolds is infinitely degenerate, of course, in the space of all vector fields (f, g) - quite like many mathematical structures are: equivariance under symmetry groups, conservation laws, integrability, symplectic structures, and many others. The special case identically vanishing g in fact amounts to standard bifurcation theory, in the presence of a trivial solution x=0. Note that this condition, which turns the k-dimensional variable y into a preserved constant parameter, is infinitely degenerate even in our present setting of equilibrium manifolds. Due to the analogies of our results and methods with bifurcation theory, we call our emerging theory bifurcation without parameters. This terminology emphasizes the intricate dynamics which arises when normal hyperbolicity of the equilibrium manifold fails. Applications include coupled oscillators, viscous profiles in systems of hyperbolic balance laws, populations dynamics, contact structures, fluid mechanics, and many more. Normal hyperbolicityNormally hyperbolic equilibrium manifolds admit a transverse C0-foliation with hyperbolic linear flows in the leaves.
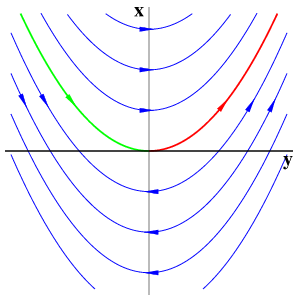
Simple zero eigenvalueThe simplest bifurcation szenario is imposed by the loss of normal hyperbolicity at x=y=0, due to a nontrivial transverse eigenvalue zero of the linearization. A normal form is given by
Clearly dx/dy=y, and the resulting flow lines are parabolas. For comparison with standard bifurcation theory, we draw the y-axis of equilibria horizontally.
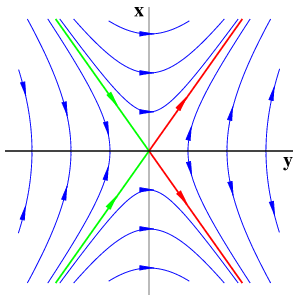
Simple zero eigenvalue with reflection symmetryThis time with an additional reflection symmetry (x is mapped to -x), we obtain a normal form
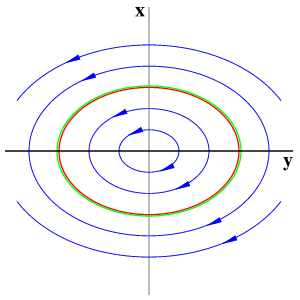
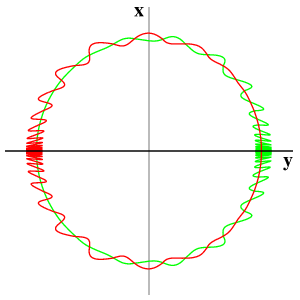
The Euler multiplier 1/x transforms the reflection into a time reversibility. Note the resulting integrable, harmonic oscillator case which originates from the elliptic sign y'=-x2 with identically coinciding strong stable (green) and strong unstable (red) manifolds.
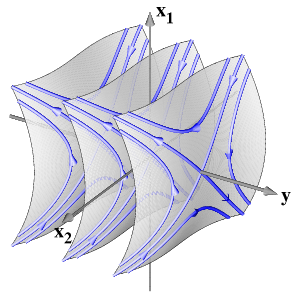
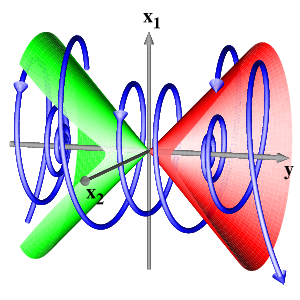
Andronov-Hopf pointIncreasing the dimension, we consider x=(x1, x2) in R2, y in R with a line x=0 of equilibria and a purely imaginary nonzero eigenvalue iw at y=0. Normal-form theory then generates an additional S1-symmetry by the action of exp(iw t) in the x-eigenspace. This equivariance can be achieved, successively, up to Taylor expansions of any finite order. In polar coordinates (r, φ) for x, an example of leading order terms is given by
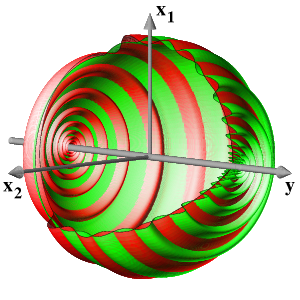
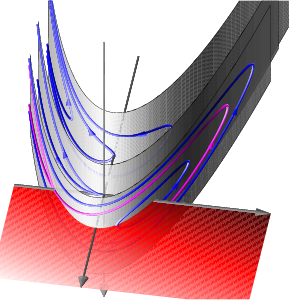
Since the first two equations coincide with the previous case, the dynamics is then obtained by simply rotating the previous figures around the y-axis at speed w. However, higher order terms typically do not respect the S1-symmetry of the normal forms. Therefore, in the elliptic case, the two-dimensional strong stable (green) and strong unstable (red) manifolds of the trivial equilibria will split, generically, to permit transverse intersections.
The final picture shows in the hyperbolic case a stable (green) and an unstable (red) cone of the bifuctation point at the origin. They separate the three regions of different behaviour. In the elliptic case, all nonstationary orbits are heteroclinic from the unstable foci, at y>0, to stable foci at y<0. In the picture, the splitting of the two-dimensional strong stable (green) and strong unstable (red) manifolds is shown.
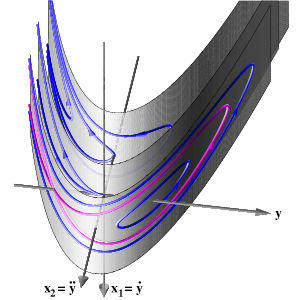
Bogdanov-Takens pointWe call a singularity with a algebraically double and geometrically simple eigenvalue zero in the cross directions a Bogdanov-Takens point, in analogy to classical bifurcation theory. This first codimension-two bifurcation requires a plane of equilibria. Alternatively, a line of equilibria with an additional scalar parameter (which does not destroy the line of equilibria) could be considiered. It turns out that, for Bogdanov-Takens points, both viewpoints lead to similar results. In suitable rescaled form a general flow near a Bogdanov-Takens point on a plane of equilibria reads
with fixed parameters b, λ and ε. The λ-y plane is the original plane of equilibria, b depends on the nonlinearity, ε is a rescaling (or blow-up) parameter. Note the algebraically triple zero eigenvalue, double in the transverse directions x=(y', y''), for λ=y=0. For ε=0 the system becomes completely integrable. Two first integrals are then given by
For fixed Θ we obtain a Hamiltonian system. The perturbation by ε>0 imposes a slow drift of these first integrals. Aiming for bounded solutions, we describe the resulting Poincaré map in a section transverse to all periodic orbits of the integrable case.
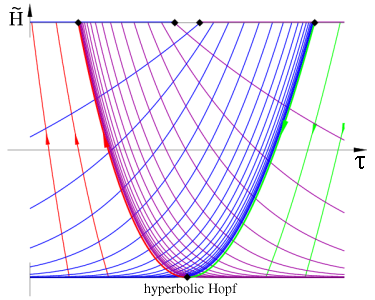
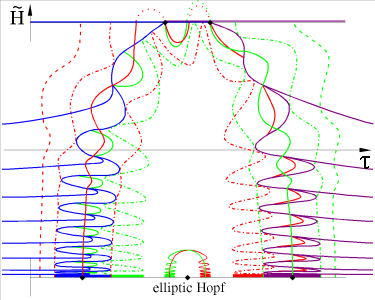
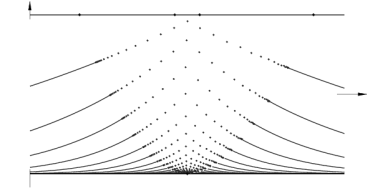
As coordinates in the section we choose τ=log Θ and ~H=Θ-3/2H, not drawn to scale. Parameters are ε,λ>0 and, for the hyperbolic case, -17/12<b<-1. For the elliptic case we consider b>-1. The equilibrium y-axis, a cusp in (Θ, H) coordinates, transforms to the top (saddles) and bottom (foci) horizontal boundaries, with y=0 relegated to τ=-infinity. Since τ and ~H are constants of the flow, for ε=0, they represent slow drifts on the unperturbed periodic motion, for small ε>0 and ~H between the top and bottom boundaries, ~H2<8/9. The top boundary also represents homoclinics to the saddles, for ε=0. Along the bottom focus line we observe Hopf bifurcations without parameters, corresponding to y=λ>0. The value of b distinguishes elliptic and hyperbolic cases. In addition, lines of saddle-focus heteroclinic orbits and isolated saddle-saddle heteroclinics are generated, for ε>0, by breaking the homoclinic sheets of the integrable case. Note in particular the infinite swarm of saddle-saddle heteroclinics, in the hyperbolic case.
References
| |||||||||||||||||||||||||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||